
RICARDO MOTTA PINTO COELHO
PROJETO 1
Curva logística
Um dos modelos de crescimento mais importantes em Ecologia de Populações, trata-se do
modelo logístico de crescimento populacional. Ele é também chamado de densidade-dependente
uma vez que a taxa de crescimento em um determinado instante depende do número de
indivíduos existente na população. Para maiores informações sobre a teoria e aplicações do
modelo, recomendamos uma leitura do capítulo 1 (pag. 21) do livro Fundamentos em Ecologia.
Consideremos uma situação formada por duas populações de organismos zooplanctônicos.
Colocamos em dois béqueres 3 fêmeas partenogenéticas grávidas de um microcrustáceo
cladócero em condições ideais de alimentação, temperatura, aeração e iluminção e ausência de
predadores. Essas duas populações cresceram muito bem atigindo respectivamente 650 e 825
indivíduos aos 24 dias.
Tabela: Abundâncias totais (número de indivíduos por litro) de duas populações de cladóceros (Daphnia laevis) em experimentos de laboratório.
| Dias (t) | População "A" (Nt) | População "B" (Nt) |
| 1 | 3,0000 | 3,0000 |
| 2 | 7,0000 | 4,0000 |
| 3 | 10,0000 | 16,0000 |
| 4 | 9,0000 | 18,0000 |
| 5 | 39,0000 | 25,0000 |
| 6 | 39,0000 | 49,0000 |
| 7 | 40,0000 | 51,0000 |
| 8 | 113,0000 | 136,0000 |
| 9 | 180,0000 | 156,0000 |
| 10 | 240,0000 | 267,0000 |
| 11 | 390,0000 | 301,0000 |
| 12 | 480,0000 | 444,0000 |
| 13 | 510,0000 | 501,0000 |
| 14 | 630,0000 | 650,0000 |
| 15 | 638,0000 | 630,0000 |
| 16 | 628,0000 | 730,0000 |
| 17 | 666,0000 | 734,0000 |
| 18 | 668,0000 | 777,0000 |
| 19 | 620,0000 | 758,0000 |
| 20 | 663,0000 | 780,0000 |
| 21 | 667,0000 | 771,0000 |
| 22 | 645,0000 | 812,0000 |
| 23 | 690,0000 | 799,0000 |
| 24 | 650,0000 | 825,0000 |
Para se determinar se estas populações se enquandram no modelo logístico de crescimento,
devemos fazer um ajuste não-linear a esse modelo. Existem várias formas de se fazer esse ajuste
(veja uma delas na página 27 do livro). Entretanto, a maneira mais fácil de se fazer isso, é através
de um bom pacote estatístico ou aplicativo gráfico-científico. Um dos melhores aplicativos,
nesse sentido, é o pacote Sigmaplot versão 2000, que vamos usar a seguir. Usaremos a rotina de
regressão não-linear que é facilmente acessada no menu "statistics" e "regression wizard". O
pacote dispõe de pelo menos 13 tipos diferentes de equações sigmóides, incluindo dois tipos de
equações logísticas que poderiam ser usadas para fazer tal ajuste. Mas, para nos mantermos fiel a
notação usada em nosso livro, optamos por usar a mesma equação que está na página 27 de nosso
livro:
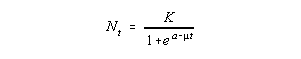
onde:
Nt é o número de indivíduos,
a, µ e K são parâmetros do modelo, sendo
µ a taxa instantânea de crescimento máximo,
ou potencial biótico da espécie e K que é a capacidade de
suporte do meio. O parâmetro "a" é uma constante de
integração. Através da opção "user defined equation" onde iremos entrar com todos os
dados necessários para tal ajuste.
Teremos então que cumprir as seguintes etapas:
A) digitar os valores de t(tempo) e número de indívíduos (Nt) em duas colunas diferentes na planilha de dados do programa e salvar o arquivo.
B) Definir qual a equação que reflete o modelo a ser usado (ver equação acima).
C) Estabelecer os valores iniciais de todos os parâmetros do modelo.
D) Estabelcer os valores de outros parâmetros acessórios exigidos pela rotina
Após essas etapas iniciais, vamos agora realizar o ajuste ao modelo logístico para as duas populações acima.
População A
Após abrir o programa Sigmaplot 2000 e recuperar o arquivo contendo os dados já digitalizados,
ir ao menu "statistics" e escolher a opção "regression wizard". Escolher a opção "user defined
equation". Inicialmente o programa solicita a definição das colunas da planilha onde estão dos
dados. Os dados do tempo (x) estão na coluna (1) e os dados dos números de indivíduos da
população A estão na coluna (2). Essas informações são digitadas na janela "variables", a seguir:
[Variables]
x = col(1)
y = col(2)
A seguir, temos que informar os valores iniciais de todos os três parâmetros do modelo que
escolhemos, ou seja, "a" (constante relativa a integração da curva),"µ" (taxa instantânea máxima
ou potencial biótico) e "K" (capacidade de suporte). Não sabemos obviamente os valores exatos
desses parâmetros, mas podemos fornecer valores que nos pareçam lógicos ou que venham da
literatura, por exemplo. O " regression wizard " do programa SIGMAPLOT 2000 abre uma
janela especial, "parameters" somente para a entrada dos parâmetros:
[Parameters]
| a | 1 |
| µ | 0,01 |
| K | 200 |
Em seguida, devemos novamente reescrever no local apropriado, na janela "equation" do
programa, a equação acima porém com a notação específica do programa SIGMAPLOT 2000:
[Equation]
f = K/ (1+ exp (a- µ*x))
fit f to y
A seguir, temos ainda que fornecer dados adicionais em duas janelas A primeira janela refere-se
a limitações de cálculo eventualmente necessárias:
[Constraints]
o nosso modelo não possui qualquer limitação.
A última janela refere-se à janela de opções:
[Options]
| tolerance | 0,000100 |
| stepsize | 100 |
| iterations | 100 |
Os parâmetros acima fornecem o limite e a precisão dos cálculos a serem efetivados. Em
modelos complexos com convergência muito demorada, tais parâmetros são de grande utilidade e
praticidade. Após termos digitado todas essas informações podemos então "rodar" a rotina de
cálculo. Após a convergência da curva, temos então os seguintes resultados:
Poder da Regressão
R = 0,99999999 R2 = 0,99999999 Adj R2= 0,99999999
Standard Error of Estimate = 0,0314
Estimativas dos Parâmetros
A seguir, o programa nos fornece as estimativas de cada um dos três parâmetros do modelo, ou seja, os coeficientes a,µ e K. Essas estimativas vêm acompanhadas do erro padrão, a estatística t e a probabilidade de que essa estatística seja ou não siginicativa. Em nosso exemplo, as três estatísticas foram significativas.
Análise de Variância (ANOVA):
Após observarmos as estatísticas R2 e as estimativas dos parâmetros do modelo, paasamos a
observar os resultados da análise de variância. Trata-se de um modelo linear que compara o
modelo de regressão adotado com o erro ou resíduo existente nos dados empíricos acima
apresentados. A ANOVA calcula uma série de estatísticas para cada um dos dois tratamentos, ou
seja, o tratamento regressão e o tratamento erro. Essas estatísticas estão em cada uma das linhas
das tabela abaixo. A ANOVA compara o poder desses dois tratamentos em explicar a variância
dos dados. Isso é feito através do cálculo da soma dos quadrados (SS). O objetivo final da análise
é o cálculo da estatística F que é obtida a aprtir da tabela abaixo:
Onde: DF= graus de liberdade, SS= soma dos quadrados mínimos, MS= (SS/DF), F= (MF
reg/MS Res), P= probabilidade de que a estatística F seja significativa.
A probabilidade nesse caso é indica que temos
99,99% de chance de que o modelo seja significativo. Podemos observar que o valor de F foi muito elevado e significativo, ou seja, que o
tratamento regressão (modelo logístico) realmente explicou a maior porção da variância dos
dados empíricos.
Estatísticas de suporte à ANOVA
As estatísticas abaixo são de suporte a análise de variância. As mais importantes referem-se ao
teste de normalidade (distribuição normal dos dados) e o teste da variância para se verificar se a
variância é constante. A análise de variância (ANOVA) é muito poderosa, porém exige que os
dados tenham distribuição normal e que a variância das médias seja constante.
PRESS = 0,0287
Durbin-Watson Statistic = 2,2645
Normality Test: Passed (P = 0,3259)
Constant Variance Test: Passed (P = 0,9400)
Power of performed test with alpha = 0,0500: 1,0000
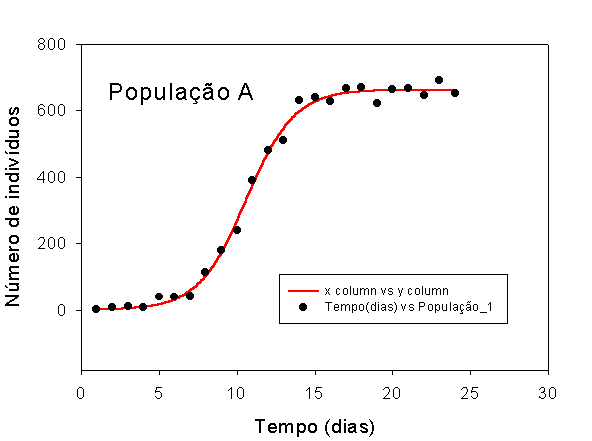
Gráfico
Finalmente apresentamos um gráfico com os valores experimentais e da curva justada. Podemos
observar facilmente que o nosso modelo apresenta uma alta aderência aos pontos observados.
Coef.
valor
Erro
padrão
Estatística
"t"
Probabilidade
"P" a
7,2104
0,0007
11034,1588
<0,0001 µ
0,6800
0,0001
10846,4006
<0,0001 K
665,0046
0,0108
61807,5241
<0,0001
DF
SS
MS
F
P Regressão
2
1937487,6126
968743,8063
982497010,1421
<0,0001 Resíduo
(erro)
21
0,0207
0,0010
Total
23
1937487,6333
84238,5928
[Nonlinear Regression]
[Variables]
x = col(1)
y = col(3)
[Parameters]
| a | 1 |
| µ | 0,01 |
| K | 200 |
[Equation]
f = K/ (1+ exp (a- r*x))
fit f to y
[Constraints]
[Options]
| tolerance | 0,000100 |
| stepsize | 100 |
| iterations | 100 |
Poder da Regressão
R = 0,99814230 Rsqr = 0,99628805 Adj Rsqr = 0,99593453
Standard Error of Estimate = 21,2020
Estimativas dos Parâmetros
| Coef. | valor | erro padrão | t | P |
| a | 5,6969 | 0,2572 | 22,1454 | <0,0001 |
| µ | 0,4861 | 0,0230 | 21,0932 | <0,0001 |
| K | 801,8288 | 9,1185 | 87,9338 | <0,0001 |
Estatísticas da ANOVA
| DF | SS | MS | F | P | |
| Regressão | 2 | 2533703,9419 | 1266851,9709 | 2818,2039 | <0,0001 |
| Resíduo | 21 | 9440,0165 | 449,5246 | ||
| Total | 23 | 2543143,9583 | 110571,4764 | ||
Onde: DF= graus de liberdade, SS= soma dos quadrados, MS= (SS/DF), F= (MF reg/MS Resl),
P= probabilidade de rejeitar a estatística F. A probabilidade nesse caso
indica que temos 99,99% de chance de que a
estatística F seja realmente siginificativa, ou seja, o modelo
logístico explica quase a totalidade da
variância observada.
Estatísticas de suporte à ANOVA
PRESS = 13949,7512
Durbin-Watson Statistic = 3,3338
Normality Test: Passed (P = 0,7440)
Constant Variance Test: Passed (P = 0,1082)
Power of performed test with alpha = 0,0500: 1,0000
A figura contendo a equação logística ajustada e os pontos experimentais da população B.
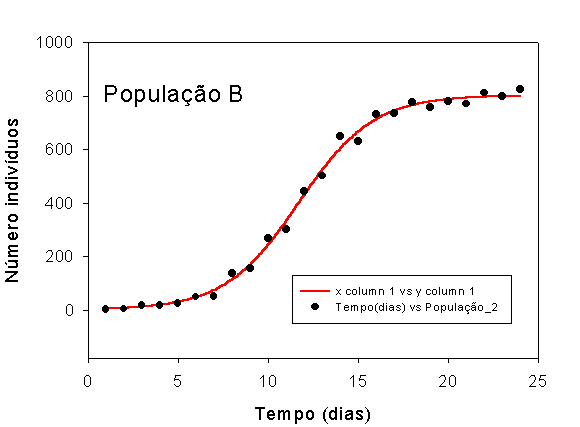
Mesmo que o aluno não disponha do programa Sigmaplot, gostaríamos de sugerir algumas atividades que o ajudarão a fixar os conceitos aqui apresentados. Em primeiro lugar, plotar os dados experimentais utilizando uma planilha convencional, MS-excel, por exemplo. Depois programar a curva ajustada aqui, calcular os valores da curva para cada dia e plotar novamente as figuras exatamente como nos dois casos acima. A planilha do excel permite realizar isso com relativa facilidade. Fazer pequenas alterações nos dados empíricos e plotar novamente os dados para observar as diferenças. Finalmente, pesquisar na literatura de suporte em que casos o modelo logístico tem sido usado com sucesso.

Página criada por Ricardo Motta Pinto Coelho
25 de junho de 2001
Dept. Ssciences biologiques
Univ. Montreal, QC, Canada.
Ultima atualização: 31/10/2016